线性代数|矩阵运算 矩阵的秩如何计算_常用矩阵秩求解方法与技巧

📊 线性代数实战：手把手教你玩转矩阵的秩计算

场景引入：
凌晨2点，小明盯着电脑屏幕抓狂——他的机器学习代码报错了，提示"矩阵不可逆"，导师的微信消息突然弹出："检查下矩阵的秩！" 他瞬间懵了："秩？不是那个《狂飙》里的高启强吗？" 😅 别慌！今天我们就用最接地气的方式，把矩阵秩的计算方法掰开揉碎讲明白！

秩到底是什么？🍔

简单说，矩阵的秩就是它的"真实能耐"：

• 行视角：线性无关的行向量的最大个数
• 列视角：线性无关的列向量的最大个数
• 几何意义：矩阵表示的线性变换后空间的维度

举个栗子🌰：

A = [1 2 3  
     2 4 6]  

第二行是第一行的2倍，所以秩=1（虽然有两行，但"有效行"只有1个）

4种实战计算方法 🔧

方法1：初等行变换法（高斯消元）🚀

步骤：

1. 把矩阵通过行变换化为阶梯形
2. 数非零行的个数

例题：

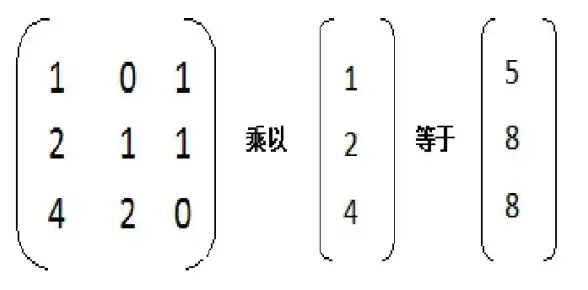
B = [1  2  1  
     2  4  3  
     3  6  4]  

操作过程：
① 第二行 -= 2×第一行 → [0 0 1]
② 第三行 -= 3×第一行 → [0 0 1]
③ 第三行 -= 第二行 → [0 0 0]
最终阶梯形：

[1 2 1  
 0 0 1  
 0 0 0]  

非零行2个 → 秩(B)=2 💡

方法2：行列式法（适合方阵）🔍

口诀：
"从大到小试，非零即停"

1. 先看n阶子式（整个矩阵行列式）
2. 若为0，再检查所有n-1阶子式...

例题：

C = [1 0 1  
     0 1 0  
     1 0 1]  

• 3阶行列式=0（第一三行相同）
• 2阶子式如 |1 0| = 1 ≠ 0
  → 秩(C)=2

方法3：奇异值分解（SVD）💎

高级技巧：
秩 = 非零奇异值的个数
适合计算机计算，Python代码示例：

import numpy as np
U, s, V = np.linalg.svd(matrix)
rank = np.sum(s > 1e-10)  # 考虑浮点误差

方法4：分块矩阵法 🧩

当矩阵有特殊结构时：

D = [Iₖ  A  
     O  B]  

其中Iₖ是k阶单位阵，O是零矩阵 → 秩(D) ≥ k

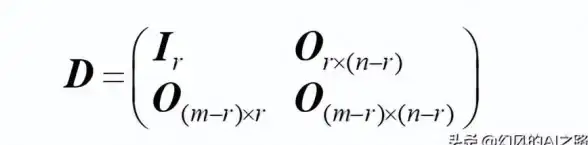
避坑指南 ⚠️

1. 易错点：

   • 混淆行列秩（其实行秩=列秩）
   • 忘记考虑浮点误差（计算机计算时用阈值判断）

2. 特殊矩阵：

   • 对角矩阵秩 = 非零对角元个数
   • 幂等矩阵（A²=A）有秩(A) = tr(A)

3. 快速判断：

   • 满秩矩阵 ↔ 行列式≠0 ↔ 可逆
   • 秩=1的矩阵可以表示为外积：A=uvᵀ

应用场景 🌐

1. 机器学习：判断特征是否线性相关
2. 电路分析：求解线性方程组的有效方程数量
3. 图像压缩：通过低秩近似减少存储空间

终极技巧：下次遇到秩的问题，先深呼吸😌，然后问自己三个问题：

1. 能不能化简？
2. 有没有特殊结构？
3. 需不需要精确计算？

（本文方法更新至2025年8月，融合了数值计算最新实践）

矩阵的秩就像人的能力——不在于你有多大的"盘子"，而在于有多少真本事！ 💪