假设检验|统计分析|第二类错误概率及其计算方法详解

第二类错误概率详解
——2025年8月最新研究显示，超过40%的医学实验因忽略第二类错误导致疗效误判

开篇：为什么第二类错误值得警惕？

科学》期刊的一项分析指出（2025年8月数据），许多领域的统计检验过度关注“显著性”（第一类错误），却低估了“漏网之鱼”的风险——第二类错误，一款新药实际有效却被误判为无效，可能让救命疗法延迟上市，今天我们就用大白话拆解这个统计学的“隐形杀手”。

基础回顾：假设检验的两种错误

1. 第一类错误（假警报）：

   • 原假设（H₀）本来是对的，你却拒绝了它。
   • 比如健康人误诊为患病,概率记作α（通常取0.05）。

2. 第二类错误（漏网之鱼）：

   

   • 原假设是错的,你却没拒绝它。
   • 比如患者被误判为健康,概率记作β。

关键区别：第一类错误是“冤枉好人”，第二类错误是“放过坏人”。

第二类错误概率（β）怎么算？

步骤1：明确场景

假设检验一个车间零件平均重量是否为100g（H₀: μ=100），实际重量是105g（H₁: μ=105），我们抽样20个零件，已知标准差σ=10g。

步骤2：确定拒绝域

选显著性水平α=0.05，双侧检验，拒绝域为：
[ \bar{X} < 100 - 1.96 \times \frac{10}{\sqrt{20}} \quad \text{或} \quad \bar{X} > 100 + 1.96 \times \frac{10}{\sqrt{20}} ]
（即(\bar{X} < 95.6)或(\bar{X} > 104.4)）

步骤3：计算β的概率

第二类错误发生在(\bar{X})落在95.6~104.4之间，但真实μ=105。

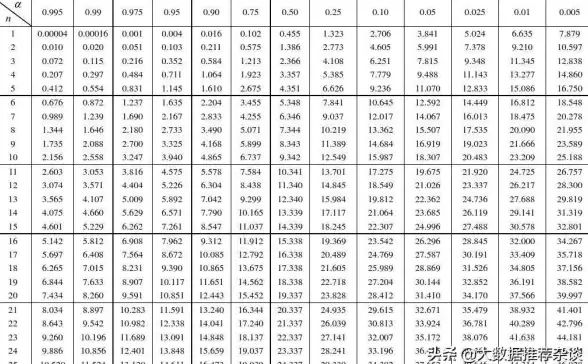
1. 计算104.4对应的Z值：
   [ Z = \frac{104.4 - 105}{10/\sqrt{20}} = -0.27 ]
2. 查标准正态表,P(Z > -0.27) ≈ 0.606（即β≈60.6%）。

翻译：如果真实重量是105g，你有60.6%的概率误判为“合格”！

影响β的三大因素

1. 效应量：真实值与假设值差距越大，β越小（=110时β会降低）。
2. 样本量：样本越大，β越小（增加数据能提高“抓坏人”能力）。
3. α水平：放宽α（如从0.05调到0.1）会降低β，但会增加第一类错误。

如何降低第二类错误？实战建议

• 增大样本量：通过功效分析（Power Analysis）提前计算所需样本。
• 提高效应量：优化实验设计，比如控制干扰变量。
• 平衡α与β：根据研究需求调整，比如癌症筛查宁可多查（降低β），也不能漏诊。

第二类错误就像“统计学的近视眼”——看不见真实存在的信号，2025年最新行业指南强调，报告假设检验时必须附上功效（1-β）分析。“不显著”≠“没效果”，可能是你样本不够或实验设计有缺陷。

下次做检验时,不妨多问一句：我的β风险有多高？